- within Food, Drugs, Healthcare, Life Sciences, Transport, Government and Public Sector topic(s)
If we want to apply the current rule of law to artificial intelligence, especially in the field of generative AI, then we need to understand what the AI models, which are the heart of an AI system, are all about. This understanding is crucial, for example, for the question of whether or not personal data is contained in a large language model, or whether the works used for training can still be found in the AI model. In this part of our AI blog series, we will explain the technical basis for such AI models; what this means legally will be discussed in the next blog post.
What generative AI does is common knowledge: It generates an output based on an AI model and an input. This can be a translation, an image or the continuation of an existing text (e.g. a dialogue with a chatbot). Many people also understand that what the often cited "large language models" do is to determine the most probable next word of an input text. In the following, we want to delve much deeper into the technological basis of this. There are very different techniques that make generative AI work the way it does, i.e. a system that generates content based on specific input and that has learned how to do so based on training. Such input and output content can be text, images, videos or audio, or a mix of all of them. The core of all these AI systems are so-called models which, together with appropriate software code and powerful hardware, are able to calculate the output based on the input. In fact, all this is indeed about maths: Having an AI model generate some texts or images is primarily an exercise where billions of calculations of algebraic equations are run.
AI models are not programmed by humans, but are trained so that they can recognise patterns and make use of the results. This concept of "trained rather than programmed" is what makes a computer system an AI – also from a legal perspective. The definition of AI in legislation such as the EU AI Act is somewhat more complex, but the only really essential component is that these systems have a certain degree of autonomy. This means that the output they generate is not calculated according to fixed rules predefined by humans, but that the programming of an AI system is "only" done to allow the model to itself learn how to generate the output and to apply this trained knowledge in a second step.
Such a system does this by accumulating a huge amounts of numbers, which it then uses to calculate the output – for example words, pixels, sounds, etc. In mathematical terms, an AI model is therefore a (complicated and multi-layered) function, a formula pre-filled with many values so to speak; it can also be represented in this way, and all the steps can be broken down into mathematical "sub-formulae", even mysterious-sounding things like a "neural network" and the "neurons" it contains. When talking about a neural network, imagine a large Excel worksheet, for example, with the neurons being the individual cells in it, arranged in several columns next to each other. Each cell displays a number that is calculated based on the numbers of all the cells in the column immediately to its left and the parameters predefined in the formula for each of these cells (with the predefined parameters being the result of the training). The input is entered in the first column on the far left and the result can then be read out in the last column on the far right of the worksheet. It has been shown that if the parameters are set correctly, this collection of neurons (here: cells) can be used extremely well to recognise patterns. The training, in turn, follows the simple principle of "trial and error": Sample inputs and desired output is used to tweak these parameters until they fit. We will explain later on in more detail how this works.
First of all, simplifications
For the sake of simplicity, we will limit ourselves here in various ways:
- We will initially only focus on the AI models and how they can work. An AI system such as ChatGPT or Copilot has various other elements, for example to recognise and filter out or block unwanted inputs and outputs (this task is performed by so-called guardrails, i.e. additional functions that check the input before it is handed over to the AI model or that check the output before it is given back to the user) or to perform tasks for which, for example, a language model is unsuitable and therefore another form of AI or other system is used (e.g. to perform calculations). Anyone offering a product such as ChatGPT will also use fine-tuning, corresponding "system prompts" (more on this later) and what is known as alignment to try to align the product as well as possible with its desired tasks (and only with these tasks). ChatGPT is therefore neither technically nor in terms of content the same as GPT3 or GPT4. A large AI language model (LLM) like GPT4 is the centrepiece of a product like ChatGPT (or Copilot), but a language model itself is not enough to create such a product. In any case, companies such as OpenAI offer other tool providers (or other companies) the opportunity to access their models directly. This is done via a so-called Application Programming Interface (API), i.e. an interface to which inputs can be sent and on which the output is then displayed after processing by the AI model in question.
- Furthermore, we limit ourselves to the so-called transformer technique. This is a method originally attributed primarily to Google, which is characterised, among other things, by a process with which the meaning of individual elements in the input can be more narrowly defined by analysing the other elements of the same input (the so-called attention mechanism). The transformer technique is the basis of AI offerings such as ChatGPT, Copilot, Dall-E, Midjourney and Stable Diffusion. GPT stands for "Generative Pre-Trained Transformer", i.e. a transformer system that has already been pre-trained to generate outputs.
- As these things are quite complicated to understand even with simplifications, we will continue to limit ourselves here to purely text-based AI models (the aforementioned large language models), for example GPT, Gemini, Llama or Mixtral. However, the same concepts are also used, for example, in image creation models (text-to-image) or models for transcribing speech (sound-to-text).
- We focus on the use of models in chatbots, i.e. systems that supplement an existing input text with a corresponding output text: The user enters an input text and the chatbot calculates the most suitable answer. It does this by calculating which is the most likely next word, taking into account the entire input and previously generated output and in view of the "knowledge" that the model has accumulated during its training (more on this in a moment). Another application of language models apart from chatbots would be the translation of text, where the aim is not to find the most probable next word, but the most probable word in the target language. In certain places, they work slightly differently. However, both are generative AI and both work with language models.
- We have thus already introduced a further simplification: We are always talking here about using a language model to determine the meaning of "words" or to predict the next "word". In reality, most language models do not work with words, but with fragments of them. They divide each sentence into many of these fragments. These are the so-called tokens. These can be, for example, punctuation marks, syllables or combinations of several syllables, parts of words or sometimes even whole words (for GPT3.5 and GPT4 see here). The tokens are the vocabulary of a language model. GPT3, for example, has a vocabulary of around 50'000 tokens. So, when we talk about ''words'' here, we mean tokens. In a model for images or sounds, tokens could stand for groups of pixels or short sequences of audio wave information from which entire images or audio stream could be built.
- When we provide figures below, we will do so for GPT3, the first major language model that became better known beyond the machine learning community when OpenAI presented its chatbot "ChatGPT" in November 2022. This also has to do with the fact that the information on GPT3 is readily available. In the case of newer language models, some providers keep their technical specifications top secret.
Functionality briefly explained
Language models such as GPT3 are built to determine the meaning of each word of the input in terms of content, style, grammarl, mood, etc. They do this by performing a whole series of calculations for each word the input, which in the end represents the meaning of the word with regard to these various aspects. If the meanings of all these words are combined at the end of all these calculations, they will point to the word that in their view is most likely to correctly continue the previous input text. This then becomes the model's output and with it, the process starts all over again, with the input now also including the word that has just been generated. In this way, the output is put together piece by piece.
The meanings assigned to the words are determined by the model, in which these meanings are stored using numbers. The model "learns" these meanings in an initial training phase, during which it is presented with countless text samples which it analyses. The Llama2 model was trained with 2'000 billion words, the recently published Llama3 with 15'000 billion words. This so-called pre-training isfollowed by the fine tuning phase, in which the model is optimised by presenting it with examples of which input should generate which output (or not). These examples can be synthetically or human generated; the amounts involved are often only a fraction of the number of texts used in the pre-training, for example 100,000. Sometimes humans are also used here, to evaluate the input-output examples (which combination is desirable, which is not) and thus help the AI model to develop its behaviour – for example the prediction of text – in the desired "direction" (the so-called alignment). All of this together can be colloquially referred to as training, even if it consists of various steps, some automatic, some manual, depending on the approach.
So, if the input consists of the words "Is the capital of France Paris?", then a language model trained on English texts will determine that the most likely next word must be "Yes". The more content a language model has seen during its training, the better it can complete the input. In a chatbot, this looks as if the chatbot is having a conversation with the user. This is because the first (usually hidden) input that the chatbot has received (the so-called system prompt) is a text such as "You are a helpful, knowledgeable assistant who has a suitable answer to all of the following questions", which is then presented to the language model as input with the first input from the user. This system prompt, some other parameters and the fact that such questions in the training content have typically been answered with more text will also ensure that the model adds a few more words beyond the first "yes" (e.g. "Yes, the capital of France is Paris.").
After training, the model is typically frozen and used in this state. This distinguishes it from the human brain, which continuously trains itself with everything we see, hear and feel. Models can also be further developed based on input collected from their users (and providers collect this data because they have an insatiable demand for training content), but this is a process that is separate from the use of an AI model (and computationally very intensive).
Technically speaking, a language model only contains numbers and no text, apart from the vocabulary of the tokens. It is therefore not comparable to a database of texts in which words can be searched for and then the individual documents seen in the training are reproduced. In principle, it is also not possible to retrieve an individual document used in training. We will see later why it is still possible that texts used in the training process can appear 1:1 in the output.
To get a better understanding of how a language model works and to understand what is stored inside it (which is very relevant from a legal point of view, among others), we will break it down into several typical steps:
Conversion to numbers and embedding
In a first step, the entire previous input (and in the context of a chatbot dialogue also the previous answers) is broken down into its components, i.e. the words (or tokens). Imagine an Excel spreadsheet, with a table where you write each word in a separate column of the first line. The maximum number of columns of this table is limited for each model. The maximum input that a model can process is known as the context. With GPT3 it was 2048 tokens, today's models in the GPT series offer context sizes of up to 128'000 tokens, the latest Gemini model from Google even up to one million. The context is important because it defines how much text the model can "look at" when determining the meaning of the individual words contained In the input. Everything that is contained in this field of view can and will be given due (but not necessarily equal) consideration by the model; anything that goes beyond this (because the input text is too long) is not considered by the model. This is why conversations with chatbots are limited in length, and why it seems that after some back and forth, a chatbot no longer takes into account what was said at the beginning of the dialogue: That text has effectively fallen out of its context, i.e. its field of view.
The size of the context has a direct impact on the computing power required to process the input, because one of the great advantages of the transformer technique is that the different meanings of all the words in the context are calculated simultaneously, i.e. in parallel, and not one word at a time (which would take forever). The calculations required for this are very simple, but very large in volume. This is why the computer chips that were originally developed for calculating screen pixels in a graphics card are used today. These are very similar calculations, and these chips are designed to perform many such calculations in parallel. This is why the graphics card manufacturer Nvidia, for example, can no longer keep up with the production of its chips in view of the current hype in genAI. So-called matrix multiplications (for example, when two tables – one with the figures of the current input text and one with the parameters stored within the model – are virtually superimposed in order to compare them) require the biggest computational effort.
Once the input text has been broken down and its words entered in the table, the coordinates that this word has in the so-called embedding space of the model are calculated for each word using the predefined values in the model. These coordinates represent the meaning that the word in question had on average across all training content. This space essentially represents the universe of all meanings that words can have. It not only has two dimensions as on a map, but in the case of GPT3 some 12'000 dimensions. For each word in the input, the Excel table in our example now retrieves the initial values from the model to determine where this word is located in this virtual space for each of these 12'000 dimensions. A set of ten words thus results in a table with a column for each word and each such column containing 12'000 rows of numbers. This matrix of numbers represents the meaning of the input. With the next steps of the process, these 12'000 values for each of the words in the input will now be adjusted over and over again.
This approach has various benefits: First, words with similar meanings will be "close" to each other in the respective dimensions. Second, relationships between words can also be represented. For example, if within this multidimensional space you "look" from the coordinates of the word "man" towards the coordinates of the word "woman", then this would be the same direction in which you would have to look to see the word "aunt" from the location of the word "uncle" or the word "female" from the coordinates of the word "male". In simple terms, this aspect of a language model allows it to for example answer the question of what the feminine form of "uncle" would be. It associates "uncle" with "male" (we will come to this in a moment) and then "travels" in this virtual space from the position of the word "uncle" using the same direction as one would take when travelling from "male" to "female". The model will then run into the word "aunt".
Determine the meaning of each word step by step
Of course, reality is much more complicated, and even identical words can have very different meanings depending on the context. This is why everything in a language model is ultimately aimed at determining the specific meaning of the input via numerous work steps.
We start with the coordinates that are stored for each word in the first level of the model and to a certain extent reflect an initial, general meaning of the word. In the subsequent steps, which basically consist of many repetitions of the same basic processes, the coordinates noted in the table for each word in the input are now continuously "adjusted" in this virtual space using the numbers stored in the model for each word and each aspect, so that with each step they reflect the word's meaning in the specific context of the input more accurately. This is done by comparing the coordinates of each word in the input with the numbers already stored in the model for each word and each aspect according to certain rules. In simple terms, in each step, a calculation is done to determine the value by which each of the 12'000 figures corresponding to the coordinates of each word needs to be increased or decreased to better reflect the word's meaning in the specific context. The position of the word in this multidimensional virtual space thus continuously shifts the more the input is analysed.
Incidentally, the experts do not speak of coordinates. Instead, they refer to vectors because vectors are the basic element of linear algebra, which is the mathematical basis of the calculations done to analyse a text and determine how to move the 12'000 coordinates of each word in the input in one direction or another based on the numbers stored in the model. A vector consists of the value reflecting the angle relative to the axis of each dimension of this space and also a length, i.e. like an arrow pointing to the position of the word in relation to such axis. If two terms have a similar meaning in one aspect, they will have a similar vector in the corresponding dimension or – if they mean the opposite – a vector that points in the opposite direction. The appropriate mathematical formula can then be used to determine a value that reflects the deviation of two vectors from each other, which can then be used to adjust the numbers in the table with the 12'000 rows for each of the words in the input.
The concrete meaning of a vector depends on the training and is not stored in prose or similar form in the model. A model does not know the objective, superordinate, universally valid meaning of the words, e.g. what the word "queen" means for people, which can be many things (queen of a state, queen of a bee colony, playing card, pop band). From a functional point of view, each vector reflects the average of the meanings that the language model has seen in the course of its training, e.g. for the word in question. If the training model is one-sided, so is the "knowledge" of the language model about the meaning of the words. However, this mode of operation also shows that thanks to this functionality a language model can generate much more output than it has ever seen in terms of training content. The training content is only (but still) needed to learn the meanings of words in texts (and their relationships) and not to memorise the training content itself; the latter is only a side effect that can occur under certain circumstances.
The advantage of this technique is that the AI model does not really have to "understand" the meaning of a word. It memorises those patterns that it has learned during training that lead most easily to the respective goal (here: correct prediction of the next word in the training materials). It memorises the patterns in the form of number sequences or a large number of number sequences (one for each word in the input) because it is very easy to calculate with such a matrix of numbers. The model does not understand these patterns itself, but it has been shown that these patterns reflect the meanings mentioned, i.e. that words with similar coordinates in relation to certain properties are also similar in terms of meaning.
At this point, some might be tempted to say that only we, as human readers of the output, recognise a deeper meaning in it and that the AI model only pretends to understand the meaning. That would be like learning a language that we don't understand but know how it is spoken in practise. The question of what "understanding" really means is, of course, a philosophical one and can be answered in different ways. It can also be argued that we humans do not process and understand language any differently than a language model does, except that we are considerably more developed and not only "understand" words in relation to each other and in their use in texts, but also link them to numerous other impressions and experiences. Language models do not do this.
Incidentally, these processes within a language model are not complex because of the algebraic formulae that are used, but because of the sheer volume of numbers that have to be multiplied, added or otherwise mathematically combined with each other in order to match the words with the numbers in the model across numerous levels. This applies to the use of a model and even more so to training (more on this below).
A question of attention
However, a language model has a few more tricks up its sleeve that make it even more powerful. The special feature of transformer models is the following concept, which has become known as "attention": it is a special procedure for further adjusting the coordinates of each word from the input in order to determine its meaning in the specific case as accurately as possible.
For each word in the input, the model "asks" all other words in the same input a question and these words "provide" an answer to this question, so to speak. If the question and answer match, this provides an impulse that shifts the coordinates of the word in certain directions in the meaning space and thus defines the meaning of the word even more precisely for the specific case. Such a question could, for example, be a search for adjectives that describe the "questioning" word in more detail. So, if we have the input sentence "He has a red, electric car" and carry out this process for the word "car", the answer for the words "red" and "electric" will match the question. Each such match in turn ensures that the coordinates previously set in the input for the word "car" are shifted in the direction of "red" and "electric". The new coordinates thus indicate that it is a red-coloured car powered by electricity.
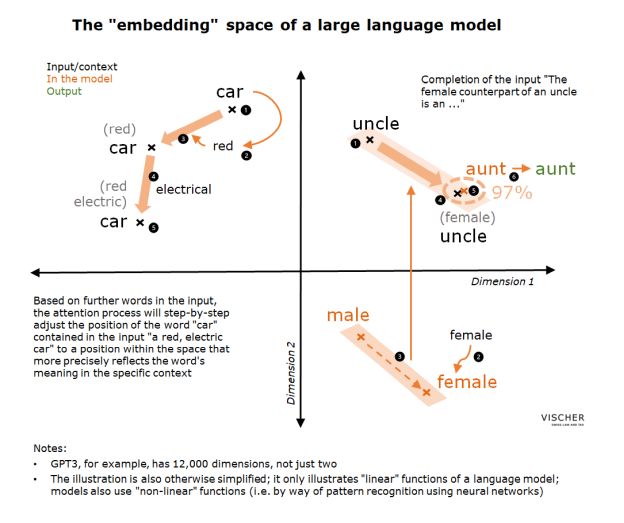
In GPT3, for each word in the input, 96 such "questions" are asked in parallel to all other words in the input (each by a so-called Attention Head) and entered in a table. The "answers" for these words go into another table. These two tables are then "superimposed" and, depending on the degree to which the numbers match (in the example: for the words "red" and "electric", because as adjectives they refer to "car", it will be high), the result (i.e. a number) will be different from the result of the answers of all other words (which do not refer to "car"). The model recognises this type of reference because it has seen these patterns many times in the training content and has, to a certain extent, stored the answers to this question for the words in question. These answers are now called up during the attention process. The result of comparing question and answer is used to calculate the necessary adjustments to the coordinates of the questioning word.
In GPT3, this process takes place over 96 levels (so-called attention layers) in order to obtain a clearer result. In this way, more meaning can be assigned to each word in the context based on the other words, i.e. the meaning of the word can be given a concrete meaning. This application is also referred to as "self-attention" because the meaning of a word is determined on the basis of the text in which the word itself is found. In language models used for machine translations, reference is sometimes made to the words found in the text of the other language ("cross attention").
Determine superordinate meanings
There is another technique in addition to the attention method, with which language models extract meanings from the input text: In the so-called Multilayer Perceptron (MLP), each word is subjected to various other tests with the aim to further determine the meaning of the input.
This involves aspects such as the language in which a word is written, whether a word refers to a specific person (rather than a thing), whether it is a number, whether it is a noun, whether it is part of a lie, whether it is part of a multi-part term or part of a quotation, the tone of a word, the relevance of a word to the text as a whole (which is important for summaries, for example), or whether it is positive or negative. For example, the statement "not bad" is positive even though it contains the word "bad". The language is important, for example, to determine the positioning of different word types: In German, the verb is typically at the beginning of a sentence, in English it usually comes later.
These meanings cannot simply be calculated in one go as with the attention method. In mathematics, one says that a "non-linear" function must be used for this purpose: To find out whether a text is part of a lie or reflects an angry mood, the pattern of the entire content must be analysed. Hence, the task can only be solved by pattern recognition; an "if-then" mechanism cannot do this. The MLP uses a neural network for this purpose, a technique that we briefly already described above. It is fed a text and, based on the patterns it recognises, it ideally provides the answers to the respective questions on which it has been trained, such as the tone of voice of the content, which language it is written in or whether it is telling the truth or not.
How a neural network works - Deep Dive
Seen from the outside, a neural network is a system that recognises patterns and can assign them to a result from a predefined series of possible classifications. We have already described how this supposed black box works in very brief terms above. If you want to understand it even better, here is a deep dive into how it works, including a description of how it is trained. The way it works is basically as simple as it is effective:
- Everything starts with a "digitisation" of the input, i.e. an image, a sound sequence or a text is converted into numbers. This has already happened in the case of a language model. In the case of images, for example, each pixel is represented by a value that reflects its colour or brightness, for example. This series of numerical values is the first level of the neural network. If the network is to process a black and white image of a number consisting of a grid of 28 x 28 pixels, this results in for example 784 values of 0 (pixel off) or 1 (pixel on).
- The numerical values from the first level are then passed on to a series of so-called neurons, which form the second level of the network. The amount of neurons varies depending on the AI model. It does not really play a role in the concept (for a simple neural network that recognises numbers from "0" to "9" in images with a reasonable degree of reliability, for example, two levels of 16 neurons and an output level of ten neurons are sufficient). Each such neuron is comparable to a cell in Excel, which contains a formula that calculates a new number from all the values present in the previous level and parameters pre-programmed in the formula. The pre-programmed parameters are, on the one hand, a series of numbers that indicate which value in the previous level should have how much "weight" in the final result shown in the cell and, on the other hand, a number with which the final result can still be influenced overall ("bias").
- The value of each neuron calculated in this way (depending on the type of network or "activation function", this can be 0.0 to 1.0 for a language model, for example) is passed on to each neuron of the next level, which contains the same formula, but each with its own series of "weights" and, if necessary, a separately stored "bias" value. This can be continued over numerous levels, with each series of neurons (i.e. the "Excel cells") passing on their calculated values to the neurons on the next level.
- At the last level, however, there are only as many neurons as the network needs to provide answers. If the network is to recognise number images from "0" to "9", it will consist of ten neurons, which in turn will use the same formula with their own weights and possibly bias values. Each neuron represents a number to be recognised. The "answer" of the network to the given task is then the neuron of the final level that contains the highest numerical value. If the network has recognised the number "2", the neuron that was assigned the number "2" during training will contain the highest number. The better the training, the higher the hit rate (provided the network is large enough). The result is also referred to as classification because it reflects what a neural network basically does: it classifies patterns, i.e. assigns them to a series of possible, predefined classes of patterns.
This network, consisting of 784 numerical values on the first level, 16 numerical values each on the second and third level and 10 values on the last level, may seem very small. However, it already contains a total of 13,002 weights and bias values that control the flow of numerical values from one level to the next (on the second level already 784 x 16 + 16 = 12,560). This means that complex patterns such as numerical images from "0" to "9" can already be recognised quite well.
With this number of parameters, it is of course no longer possible to set the correct weights manually. That is what training is for. This teaches the network which types of patterns it should recognise in the input and what constitutes these patterns. In principle, this also works quite simply:
- At the beginning, the weights and bias values in the formula of each neuron are set randomly.
- The network is shown an initial pattern (e.g. the image of a number in the case of number recognition). At the last level, the network will provide random numerical values (i.e. random classification), as it is still completely untrained. Because the number that should appear is known, we now calculate for each neuron at the last level how much the numerical values actually delivered (i.e. from 0.0 to 1.0) must be corrected so that the result would be accurate, i.e. the neuron that stands for the number shown (e.g. "2") contains a 1.0 (it is "activated"), and all other neurons contain a 0.0. If the neuron that stands for the number shown contains a 0.5, 0.5 must be added so that it is activated. If there is already 0.8, only another 0.2 would be necessary. This correction value is referred to as "loss" or more classically as "cost", similar to the costs incurred for the subsequent correction of the bad result.
- Using these "losses", further mathematical formulae can now be used to determine how the weights and the bias value in the neuron's formula should ideally be adjusted so that the result at the last level would be correct.
- This process is carried out backwards across all levels, so to speak, and the weights and bias values are adjusted at each level. This process is also known as backpropagation and is a challenging calculation process simply because a large number of values have to be calculated.
- Steps 2 to 4 are repeated with numerous other inputs (here: number images) and correct classifications of the inputs (here: the numbers they represent). Over time, the "losses" decrease and the neural network becomes better and better at recognising the trained patterns (here: numbers on the number images). The person training the model does not need to tell it or programme it how to recognise a number (e.g. a round or circular element or a vertical line). With enough practice, the model will find out on its own. It is interesting to note that even if the weights contained in the neurons or the numbers calculated on the various levels are visualised, the numbers ("0", "1", "2" etc.) or their graphical components cannot be recognised when looking at these visualisations. In other words, a neural network does not simply store images that it then compares. At the same time, this property makes it difficult for humans to understand how the network gets to a specific result. In addition, a neural network does not know what a certain number really is. If it is shown something other than a number, a certain neuron may still be activated at the last level, i.e. it may nevertheless provide a (wrong) answer. Because it has only been trained on numbers, it does not recognise when it is presented with something else, or when the numbers are presented in a way that differs greatly from the training material (e.g. a "3" lying down instead of standing upright).
Back to the text – and the temperature thing
In the MLP and thereafter, the above steps are carried out several times in succession. Each time, the coordinates for each word in the input are adjusted slightly and take on more nuances of the input with each step. Ultimately, each word is set in relation to all other words, a distinction is made between relevant and less relevant words, and the overall meaning of the words is determined as far as it results from the input (and the output generated so far), with the scores ultimately coming from the training content and manual optimisation.
Which word follows the words in the input can be determined relatively easily in the last step of the process by offsetting all remaining coordinates against each other, so to speak. The result are the coordinates of one single point in the virtual space. The words that are closest to this point in the space are the candidates for the most likely next word. The model then creates a list of these candidates and calculates the probability of each one. The closer they are to the final point in the space, the higher their share of the total 100 per cent to be "distributed" among the candidates in this process. The word with the highest percentage is then output.
This is where the so-called temperature comes into play, an important (but not the only) parameter that influences the output of the model. Temperature is a parameter that is added to the formula for calculating the aforementioned probability distribution of the various candidates for the most probable next word. The higher the temperature, the more evenly the 100 per cent probability is distributed across the various candidates (whereby an even distribution corresponds to a random guess, i.e. what a model would output without training). The lower the temperature, the higher the probability calculated for the word that is "closest" to the final coordinates. If the temperature is very low, the 100 per cent to be distributed will lie almost entirely on the word closest to the endpoint and this word will win the competition. The temperature can therefore be used to vary the generation of the next word from deterministic (so-called greedy decoding) to completely random. Experience shows that it is not necessarily the best choice to generate texts with a temperature of 0. It is often possible to generate better quality texts with a slightly higher temperature.
The temperature can also be a reason for the so-called hallucinations that a model produces by inventing things that are not true. Hallucinations are not always undesirable. In positive terms, temperature can also be used as an instrument for more creative outputs. For example, if you feed a language model the beginning of a classic children's fairy tale that the model has already seen numerous times, it will receive the classic continuation of this fairy tale at a temperature of 0. Choosing a higher temperature allows the model to deviate from the line of text it has learnt. Once it has made a deviation, it may take completely new directions because it is working its way forward word by word: As soon as a new word is selected with which to continue the input, this new word is added to the input, and the whole process begins again with the text supplemented by the new word.. The new word can give the previous input text a completely new meaning, and the output will deviate more and more from the "usual" course of the story as found in the training materials.
Of course, temperature is not the only reason for errors in the output of a model. Because the model generates its output based on the meaning it has (correctly or incorrectly) extracted from the training content, it can also reproduce these incorrect meanings in its output if there are errors in this content. Or certain words or word combinations in the input can provoke a "deviation" from the sequence of words expected by the user because they trigger some other meaning in the model. None of this can really be predicted today; the possible combinations are simply too large for that.
We can build them, but we don't really understand them
However, it also follows from the above that the more parameters a model has, the more balanced and better it can generate texts (or other outputs). This is because more training content means that it can determine the meanings of the words more reliably at all levels. It's like a study: the result of a study with 20 measuring points is less reliable than the result of a study with 200 measuring points, even if the measuring points have been selected as equally as possible in both cases. This is why it is so important for the reliability of AI models to be fed with as much different training material as possible. The more such material there is, the statistically lower the probability that it will reappear in the output, because a model already "neutralises" the individual content to mean values or "normalises" its meaning due to the way the model works.
This is also important because the purpose of a large language model is normally not to simply reproduce the content learnt (which would be technically possible), but to derive meanings from the content, which can then be used to construct any amount of different content. For this reason, anyone training such a model is typically interested in repeating the same content as little as possible, but instead presenting the model with as much different content as possible. This improves the model's ability to generate new high-quality output based on the respective input. The aim of a large language model is therefore to invent text based on the semantic knowledge gained from the training content.
However, even top scientists in this field are still unable to explain some of the phenomena that can be observed in large language models. For example, why they can manifest what appears to be a "self healing" behaviour during training, which in the scientific community is described as the so-called double descent phenomenon (because the "loss" goes down, then up and down again). Or how AI models can sometimes solve tasks for which they have not consciously been trained (known as generalisation). Or how a particular problem-solving skill does not manifest itself gradually but appears suddenly and unexpectedly in the model (so-called grokking). Or whether grokking and double descent, for example, are actually the same phenomenon.
All these phenomena and more occur, and experts are still puzzling over why this is the case. In other words, although mankind is able to build ever larger language models that do amazing things, we still don't really understand exactly why they produce what and when. Just as other scientific disciplines such as physics or chemistry first tried to understand how the world works through experimentation, today's deep learning scientists are also trying to find out through trial and error how large language models work and why they do what they do. At first glance, this may set alarm bells ringing because it indicates that we are using a technology that we basically do not understand. At the same time, however, it must be emphasised that large language models more often than not surprise us with better performance than expected. We will discuss what this all means for the often cited requirement of AI results to be "explainable" in a separate blog.
For practical use, at least in critical applications of large language models, this means that not only adequate tests are needed to test the suitability and reliability of these models for the specific case. Their use must also be monitored in order to identify undesirable behaviour in practice. And in some cases, it may also be appropriate to use smaller language models with less complexity and skills, for example when it comes to very specific tasks (such as recognising certain content in texts that is to be redacted or blocked). Smaller models also have the advantage that they require less computing power and memory – and less energy.
Store content without storing text
It is clear from the above description that a language model does not contain any specific texts, at least not in the classical sense. However, starting from any input, it can generate concrete texts by imitating the concepts identified in the training content and thus generate texts that that can be applied in the respective individual case and have the same meaning as the texts from the training.
Although a language model does not store any of its training texts as such, it is still possible for them to be extracted. This has to do with the fact that the parameters that store the meaning of words are, in combination and under certain circumstances, also able to store content. The most important of these circumstances is how often a particular text has been seen in training. Other factors are the length of a text and how large the model is, i.e. how many parameters it has.
If a text has been seen very often in the training content, then the model will presumably complete it in exactly the same way when it is presented with the first part of the text. The sentence "A cat has nine" can intuitively only be continued in one meaningful way; we have heard or read the proverb many times. This will also be the case for a large language model trained on English texts. This has nothing to do with the fact that the language model has been presented with the same document several times. On the contrary: when training language models, care is usually taken to ensure that the same or very similar documents ("near duplicates") are filtered out ("deduplication"). For the reasons already mentioned, each text should only be used once if possible. However, such phrases, commercial or political slogans, certain name combinations, popular quotes or other texts, such as the wording of an open source licence often used in computer programs, a celebrity's CV or date of birth, or a news story, can appear in roughly the same way in many different documents used for training.
In this way, certain knowledge is engraved in the language model. Because the meaning of each word is also derived from the meanings of the other words, and from the very specific combination of the other preceding words, the model "knows" that the words "birthday", "Donald" and "Trump" are typically followed by the words "14th", "June" and "1946". Conversely, in the model, the meanings of the words "June", "1946" and "born" do not necessarily point to the words "Donald" and "Trump". It is therefore much less likely that the model can say that in June 1946 Donald Trump was born than that it can name Donald Trump's birthday. So does it know Donald Trump's birthday? Yes and no, it depends on how the question is asked, i.e. what input is provided to the model. This will be relevant for the data protection issue of whether a large language model contains personal data; we will discuss this in a separate article.
It is, of course, also possible that incorrect information can be fed into a language model in this way, or that the model does not recognise the meaning of a word because it has occurred too rarely in its training content. This is another reason why there may be an interest in feeding such models with as much different and high-quality content as possible: It is a strategy to reduce the influence of individual pieces of incorrect information on the "knowledge" stored in the model. For the same reason, it can also be useful to consciously ask a language model whether a piece of information is correct. This question alone can trigger the model to allow itself to be more strongly influenced by the knowledge based on texts that have dealt with the correctness of a particular statement when generating its answer.
It is, however, still not really possible to explain why one particular input leads to a particular output, at least with the very large language models. The question of how often a text has to appear in training for it to be reflected in the output also remains unanswered to this day. The individual words in the context pass through too many levels, their coordinates in the virtual "space" discussed above are adjusted too frequently, so that it is very difficult or even impossible to predict this, even if all the parameters of a language model are theoretically known – after all, they no longer change during use, as soon as training is complete.
Like a set of magical dice
According to what has been said, it is therefore impossible to tell just by looking at a model what output the language model will generate in response to a particular input. A language model could thus also be described as a set of magical letter dice with a movable weight built into each cube. A hidden mechanism can move this weight in any direction within each cube. If it is positioned in the centre of the cube, the letters thrown are random. However, if the thrower announces something (= input) before the rolling the dice, the mechanism automatically moves the weight in each die in one direction or the other based on this announcement. If the dice are then thrown, they always land with a certain side up and thus display a text (= output). The dice do not show which words can be formed with them, and it is also not possible to predict exactly how the mechanism works. Which letters it displays and when can only be determined by trial and error – and in any number of combinations.

This analogy is also appropriate for another reason: the majority of the parameters contained in a large language model are also referred to in technical jargon as so-called weights; we are already familiar with this term from the above explanation of how neural networks work. These are numerical values that are stored in the model and ensure that the coordinates of the various words in the input shift in one direction or another while the input is moved through the many processing levels that each model consists of. Large language models have billions of these weights spread across all these processing levels.
All of these weights must be correctly adjusted and harmonised through extensive training so that as a whole they fulfil their purpose. This applies not only to the weights that are stored in the neural networks of the language model. The principle is similar to that described above for a neural network: The model to be trained is not presented with the training content in its entirety, but only word by word. After each word, it is asked to predict the next word. Based on the word that actually follows next in the training content, the various weights and other parameters contained in the model are then readjusted so that it can perform this task better the next time. In this way, with each training content, the model gains an "intuition" (to avoid using the word "knowledge") for texts in the style and manner of the training content, which is stored in the combined set of weights and other parameters.
What does this mean for data protection?
With this, we hope we have provided an initial foundation for a better understanding of what happens in an AI model when it generates texts, for example.
We would also like to take this opportunity to thank Imanol Schlag from the ETH AI Centre for his technical input on this article.
In our next blog post, we will explain what this means from a data protection perspective and how data subjects' rights can be asserted against this background. We have already explained what all this means for users from a copyright perspective in Part 14. And in another blog post, we will explain the legal requirements for the training of language models.
The content of this article is intended to provide a general guide to the subject matter. Specialist advice should be sought about your specific circumstances.

